VSWR, ການສູນເສຍຜົນຕອບແທນ (RL), ພະລັງງານສະທ້ອນ, ແລະພະລັງງານຖ່າຍທອດ

ການພົວພັນລະຫວ່າງອັດຕາແຮງດັນຂອງແຮງດັນ (VSWR), ການສູນເສຍກັບຄືນ (RL), ພະລັງງານສະທ້ອນ, ແລະພະລັງງານທີ່ສົ່ງຜ່ານແມ່ນເຊື່ອມຕໍ່ກັນໂດຍຜ່ານຄ່າສໍາປະສິດການສະທ້ອນ (Γ). ຂ້າງລຸ່ມນີ້ແມ່ນສູດຫຼັກ ແລະຂັ້ນຕອນສໍາລັບການປ່ຽນໃຈເຫລື້ອມໃສ:

### **ສູດ​ຫຼັກ**
1. **ຄ່າສໍາປະສິດການສະທ້ອນ (Γ)**:

\Gamma = \frac{\text{VSWR} - 1}{\text{VSWR} + 1}

2. **VSWR** ຈາກ Γ:

\text{VSWR} = \frac{1 + |\Gamma|}{1 - |\Gamma|}

3. ** ການສູນເສຍກັບຄືນ (RL)** ໃນ dB:

\text{RL (dB)} = -20 \log_{10}(|\Gamma|)

4. **ພະລັງງານສະທ້ອນ (%)**:

P_{\text{ref}} = |\Gamma|^2 \times 100\%

5. **ພະລັງງານຖ່າຍທອດ (%)**:

P_{\text{trans}} = \left(1 - |\Gamma|^2\right) \times 100\%

---

### ** ຂັ້ນຕອນການແປງ **
#### **1. ເລີ່ມຕົ້ນດ້ວຍ VSWR**:
- ການ​ຄິດ​ໄລ່ Γ​:

\Gamma = \frac{\text{VSWR} - 1}{\text{VSWR} + 1}

- ໃຊ້ Γ ເພື່ອຊອກຫາ RL, ພະລັງງານສະທ້ອນ, ແລະພະລັງງານການຖ່າຍທອດໂດຍໃຊ້ສູດຂ້າງເທິງ.

#### **2. ເລີ່ມຕົ້ນດ້ວຍການສູນເສຍຜົນຕອບແທນ (RL ໃນ dB)**:
- ການ​ຄິດ​ໄລ່ Γ​:

|\Gamma| = 10^{-\text{RL}/20}

- ໃຊ້Γເພື່ອຊອກຫາ VSWR, ພະລັງງານສະທ້ອນ, ແລະພະລັງງານສົ່ງ.

#### **3. ເລີ່ມຕົ້ນດ້ວຍພະລັງງານສະທ້ອນ/ສົ່ງຜ່ານ**:
- ສໍາລັບ **ພະລັງງານສະທ້ອນ** (\(P_{\text{ref}}\)):

|\Gamma| = \sqrt{\frac{P_{\text{ref}}}{100}}

- ສໍາລັບ **ພະລັງງານຖ່າຍທອດ** (\(P_{\text{trans}}\)):

|\Gamma| = \sqrt{1 - \frac{P_{\text{trans}}}{100}}

- ໃຊ້Γເພື່ອຄິດໄລ່ VSWR ແລະ RL.

---

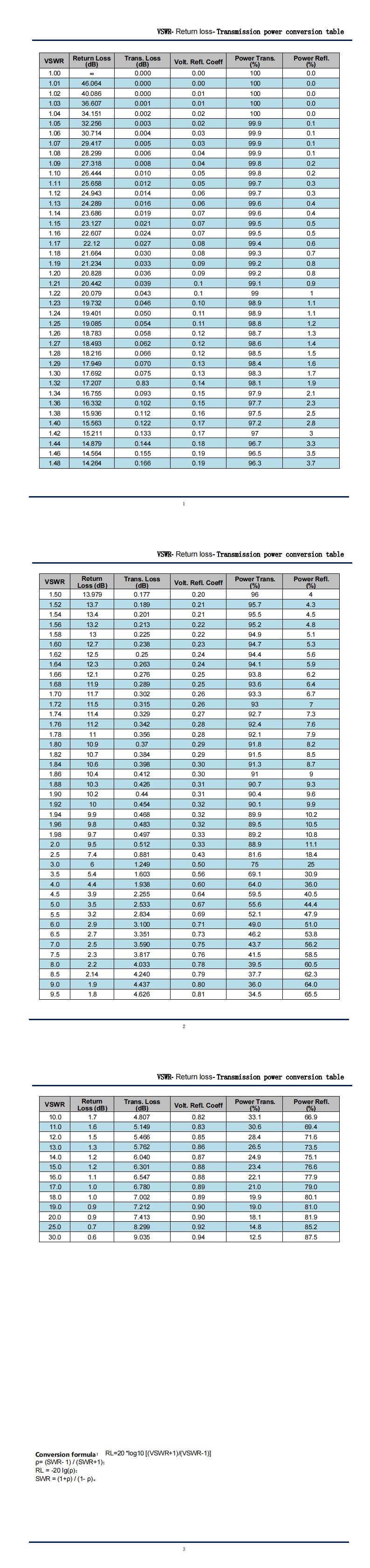
### ** ຕາຕະລາງຕົວຢ່າງ**
| **VSWR** | ** ການສູນເສຍຄືນ (dB)** | **ພະລັງງານສະທ້ອນ (%)** | **ພະລັງງານສົ່ງຜ່ານ (%)** |
|----------|----------------------------------------------------------------|--------------------------------|
| 1.0 | ∞ (ການຈັບຄູ່ທີ່ສົມບູນແບບ) | 0% | 100% |
| 1.5 | 14.0 dB | 4% | 96% |
| 2.0 | 9.5 dB | 11.1% | 88.9% |
| 3.0 | 6.0 dB | 25% | 75% |

---

### **ໝາຍ​ເຫດ**
- A **VSWR ຂອງ 1:1** ຫມາຍຄວາມວ່າບໍ່ມີການສະທ້ອນ (Γ = 0, RL = ∞).
- ** VSWR ສູງ ** ຫຼື ** RL ຕ່ໍາ ** ສະແດງເຖິງພະລັງງານທີ່ສະທ້ອນໃຫ້ເຫັນຫຼາຍ.
- **ກຳລັງສົ່ງຜ່ານ** ຂະຫຍາຍສູງສຸດເມື່ອ VSWR ≈ 1.

ໃຊ້ສູດເຫຼົ່ານີ້ເພື່ອປ່ຽນລະຫວ່າງຕົວກໍານົດການສໍາລັບການຈັບຄູ່ impedance ໃນລະບົບ RF.